A strategy known as 'Markov' is one that relies solely on state variables that provide an overview of the game's previous play. One example of a state variable is the current play in a game that is being played repeatedly. It is said to be a Markov perfect equilibrium for a profile of Markov strategies if it is also a Nash equilibrium in each and every state.
A Markov perfect equilibrium is a state of affairs that can only be achieved in computer games. This equilibrium occurs when the strategies employed by each player in a stochastic game are identical to those utilised by the other players. It is possible to define it as a collection of different strategies for each player that satisfies the criteria that is derived from the criteria that are listed below:
In game theory, the concept of Markov perfect equilibrium serves as an example of an equilibrium state. The fields of political economy, macroeconomics, and industrial organisation have all made use of it in their research. The first published use of the term dates back to around 1988 and was found in the writings of Jean Tirole and Eric Maskin. The idea of subgame perfect equilibrium was later developed further into what is now known as Markov perfect equilibration.
Google's search engine would not be nearly as successful without the PageRank algorithm. How does Google determine which of the billions of web pages it indexes have the highest PageRank? Is it possible for a computer programme to emulate a game of Google-opoly while also performing network browsing? The correct response is 'no,' but the method that is applied yields results that are equivalent.
The computation in the applet uses GT solely for the purpose of saving space within the applet. As a consequence of this, you come across a column vector rather than a row vector, as was described in the preceding text. When applied to each row using the same logic, the expression mathbfv nT is produced when n gets larger.
With the help of the Markov transition matrix, we were able to determine the steady-state vector for the network's PageRank. According to the entries, if we surf the internet for an infinite amount of time, we will end up on web page 1 26.6% of the time. If we were to randomly surf the web, it would take more than 50 rolls of the dice for us to come up with the same PageRank for the system.
In the field of game theory, symmetric games are games in which each player has a strategy and action set that are symmetrical to those of the other players.
Equilibria are stable with respect to large changes in payoffs, but this is not the case for changes of a smaller magnitude. It is possible to use a state that has a negligible impact on payoffs as a signal carrier; however, if the payoff difference between the state in question and any other state becomes null, the state in question must be merged with the other state.
The cost of a plane ticket for a particular route is the same regardless of whether it is purchased from Airline A or Airline B. A general equilibrium model that is realistic is unlikely to produce results that are nearly identical to existing prices. Both airlines have already committed to providing service by making substantial investments in the necessary infrastructure (equipment, personnel, and legal framework).
In the event that two airlines charge different prices for their tickets, the airline that charges the higher price will not sell any tickets. This approach is known as a Markov strategy due to the fact that it does not rely on a record of previous observations. If both airlines adopted this strategy, a Nash equilibrium would result in each and every one of the relevant subgames.
Within the context of an oligopoly, the Markov perfect equilibrium model is able to assist in shedding light on tacit collusion. It makes it possible for us to make forecasts regarding the actions taken by the airlines in the event that the outcome is invalidated. According to the authors' assertions, the punishment justification is further removed from the empirical account than the market share justification is.
For systems with the Markov model approaches, this indicates that the subsequent state is state dependent and is independent of all previous states at any one time. When the system being represented is independent and is not impacted by an outside agent, two types of Markov models are frequently utilised.
Sincere attempts have been made to analyse evolutionary games using the Markov chain method, but this has never been done in a systematic or sustained manner. The Markov chain has connections to key ideas in evolutionary games like fixation probability, conditional fixation time, and stationary.
A strategy can replace its offspring and be replaced by another strategy in an evolutionary game. The frequency of one strategy rises by one in each step, while the frequency of another strategy falls by one. The evolutionary game's update rule determines which tactic has a higher chance of reproducing.
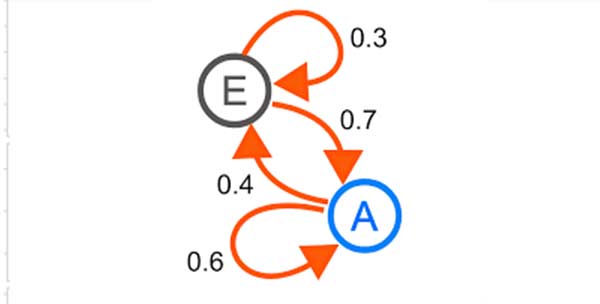
An example of a Markov model that is used to represent systems where all states are observable is a Markov chain. Markov chains display every possible state as well as the transition rate, or the likelihood of switching from one state to another in a given amount of time, between each state. Applications for this kind of model include speech recognition and market crash forecasting.
To represent systems with certain unobservable states, hidden Markov models are used. They are employed in many different fields, such as thermodynamics, finance, and pattern recognition.
Andrey Andreyevich Markov lived from July 20, 1922 to June 14, 1856 In Russia. His contributions to the theory of stochastic processes—later known as Markov chains and the Markov Strategies are what made him most famous. They demonstrated the disparity between the Markov brothers. Andrey Andreevich Markov, who was his son, was also a well-known mathematician.